J-DSP Lab 5: The Fast Fourier Transform (FFT)

Lab 5 concentrates on the Fast Fourier Transform (FFT).

Problem 5-1: FFT Properties

Consider the symmetries in the following signals. We want to see how these symmetries affect FFT spectra.

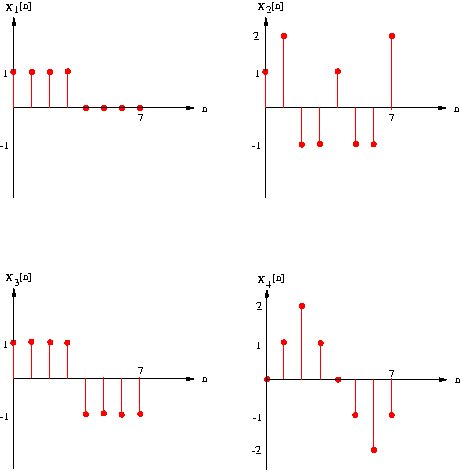
1. Generate the given signals in J-DSP and plot the FFT of size N=8.

Note: In the Sig Gen block dialog box, set the “signal” to Self-Defined and an [Edit Signal] button will appear. Click the [Edit Signal] button and enter the index along with the desired value of the signal at that index. Click the [update] button for the change to take effect. The new value is then shown in the table.

2. For which of these FFT plots is the real (imaginary) part zero?

Problem 5-2: The Rectangular Window

In this exercise we want to see the effect of truncation on the FFT spectra. We will subsequently try tapered windows as well. Generate a sine wave of “gain” 1, “pulse width” 128 samples, and “time shift” 0, with ”frequency” p/10 = 0.1 p.

Window (truncate) the sine wave for both cases below and plot the FFT of size N=128 for both cases (use dB scaling).

i) A rectangular window of length 64 samples (what does this represent? zero padding?)

ii) A rectangular window of length 128 samples (is the sinusoid resolved exactly?)

Plot the FFT of size N=128 for both cases (use dB scaling).

iii) Repeat i) and ii) for “frequency” p/11.

Compare the outputs between each of the four cases. Explain the differences in the FFT magnitude plots. Think of the effects of the windows and zero padding; also try to figure out the frequencies that the 128-point FFT can resolve exactly.

Problem 5-4: Window Tradeoffs

Generate the following signal

Window x(n) with

i) A rectangular window of length 128

ii) A Hamming window of length 128

Using J-DSP, plot the FFT of size N=128 for both cases (use dB scaling). Why is the shape of the FFT different? Which window would you choose and why?